今天大家开始讲因式分解。以我对初中数学的理解,因式分解学通了,那样整个中学阶段所有些计算你都过关了,这个说法毫不夸张换句话说,这是决定你计算能力巅峰的一个章节。然而在学校里,目前这个内容分配的课时和它在整个中学习数学中的地位是不相称的。所以我将用非常长非常长的篇幅来详细解说因式分解及其延伸常识。有人会说是否小题大做?你若是仔细研究一下高考考试数学的大题,尤其是分析几何和函数的题目,简直就是各种因式分解的运用,这是直接的联系;至于间接联系那就不胜枚举了,甚至到了大学学高等数学的不定积分的时候,还要用因式分解来进行裂项呢。因式分解的办法有不少,最根本的就是:公式法。多项式的乘法是种非常有意思的运算。除法当然是它的逆运算,而因式分解也可以看成是一种逆运算。而逆运算的重要程度前面已经说过了,这里就不再讲了。你!想!得!美!逆运算对于计算的检查来讲肯定是神兵利器!用相同的办法检查是大忌!检查最好的方法就是逆运算而不是:一!题!多!解!要紧的事情不要说三遍,三十遍贼老师都能给你念叨过去。不是我上年龄爱唠叨。有喜欢乒乓球运动的父母了解,高手的成长过程中,机械地重复一个技术动作是再平时不过的事情,通过成千上万次地训练,让肌肉产生记忆,动作不会变形。同样的,对于要紧的理念,在整个系列中我会时不时地提起,确保作为父母的你把这种正确的理念传递给孩子。
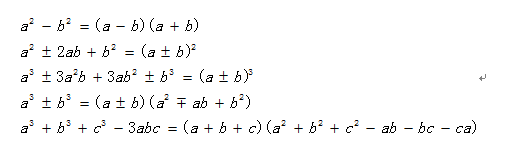
什么?就这么点?对啊,就这么点,欧几里得五个公设还搞出了平面几何呢。。。所以不要看不起这几个公式,组合在一块就是千变万化当然,这里还有一些其他的分解方法。最基本的叫分组分解法。我一直强调的是,任何办法、定义、概念、定理,必须要抓住其本质。所谓的分组分解,就是指待分解的因式经过肯定的排列组合之后,可以提取出公因式来。没错,敲黑板划重点:公因式。所以,这确实是因式分解里最简单的一种由于你只须花点笨力气,就肯定能做出来。譬如大家先来看因式分解:
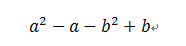
只须你有把子力气,就能进行多次尝试:
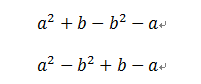
这不就试出来了?当然,这不是大家的终极目的,大家期望的是:一次成型!这个,有困难程度。大家了解,数学难就难在你在做题目的时候是不会有这么明确的指向的。那样多方法综合运用,我如何了解该用哪种办法,该如何分组?!问题是你连简单的都没练好,如何可能复杂的能看穿呢?就分组分解法来讲,或者再具体一点,就上面这个例子,大家看到这个式子里有两个字母,所以假如你把所有些字母都岔开,分成的组各包括一个字母,就像题目本身那样,这个肯定是不对的分解方法一组只包括字母a,一组只包括字母b,公因式?连字母公用都办不到。第二,次数相同的尽可能在一块。对于高次的多项式,大家有平方差立方差,立方和等等公式首要条件是大伙次数是相同的项凑在一块,即所谓的齐次多项式。大家所有些公式里是没高低次幂混搭在一块走波西米亚风的,肯定是整整齐齐的。有了这两条,直接就能把正确的分组状况给写出来了。大家再来看一个。
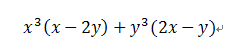
根据之前所讲的方法,第一把字母岔开,然后齐次项。。。等等,这个就是齐次多项式啊?!这就是传闻中的稍微变一变就束手无策?齐次多项式不假,这时大家还有个对称性的想法,一直和考虑的嘛:原式
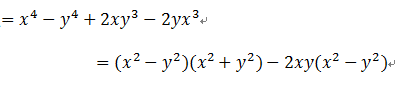
剩下的就好办了。最后再来一个携带化归的分组分解:
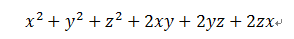
既然叫分组分解,那样这时又该如何解决呢?这时仿佛前面讲的又用不上了。。。数学永远就是这么尴尬。那这时该如何解决?想想自己手上有哪些!(字数太多打感叹号太累了)既然这个多项式一个减号都没,那样大家的公式可用范围立马缩小了;而且这个多项式是二次的,那样所有立方的公式也用不了了;于是只剩下和的平方的公式了。是否非常合理?然而和的平方的公式只有三项啊!而且只有两个字母啊!那就先挑出三项只有两个字母满足和的平方的公式再说啊,大家把式子改写成:

先把前三项用起来:
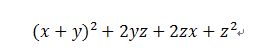
大家发现,中间两项又有公因式了。什么?为何不需要最后两项?不对称,看了难受。。。
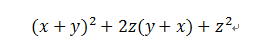
这时,答案呼之欲出了,把x+y当成一个整体之后,这又可以走一波和的平方的公式了!
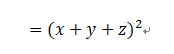
父母在指导分组分解的时候,必须要注意几个原则:字母岔开、对称、手上的工具!不要光说多试一试,再看看。要明确告诉孩子如何试,如何看。就算是没头绪地进行尝试,也要让孩子有顺序地试,就像
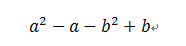
的分解过程那样尝试,保留所有尝试的记录,不要重复尝试,也不要遗漏。贼老师,如何又是不重复,不遗漏?你,上道了。